Table of contents

Appendices

4.2 Rectangular Areas

Area Types[top]

There are two types of areas: block-areas and inline-areas. These differ according to how they are typically stacked by the formatter. An area can have block-area children or inline-area children as determined by the generating formatting object, but a given area's children must all be of one type. Although block-areas and inline-areas are typically stacked, some areas can be explicitly positioned.

A line-area is a special kind of block-area whose children are all inline-areas. A glyph-area is a special kind of inline-area which has no child areas, and has a single glyph image as its content.

Typical examples of areas are: a paragraph rendered by using an fo:block formatting object, which generates block-areas, and a character rendered by using an fo:character formatting object, which generates an inline-area (in fact, a glyph-area).

Common Traits[top]

Associated with any area are two directions, which are derived from the generating formatting object's writing-mode and reference-orientation properties: the block-progression-direction is the direction for stacking block-area descendants of the area, and the inline-progression-direction is the direction for stacking inline-area descendants of the area. Another trait, the shift-direction, is present on inline-areas and refers to the direction in which baseline shifts are applied. Also the glyph-orientation defines the orientation of glyph-images in the rendered result.

If the reference-orientation for an area is 0, then the top, bottom, left, and right edges of the content are parallel to those of the area's parent and consistent with them. Otherwise the edges are rotated from those of the area's parent as described in [reference-orientation] . The inline-progression-direction and block-progression-direction are determined by the location of these edges as described in [writing-mode] .

The Boolean trait is-reference-area determines whether or not an area establishes a coordinate system for specifying indents. An area for which this trait is true is called a reference-area. Only a reference-area may have a block-progression-direction which is different from that of its parent. A reference-area may be either a block-area or an inline-area.

The Boolean trait is-viewport-area determines whether or not an area establishes an opening through which its descendant areas can be viewed, and can be used to present clipped or scrolled material; for example, in printing applications where bleed and trim is desired. An area for which this trait is true is called a viewport-area.

A common construct is a viewport/reference pair. This is a viewport-area V and a block-area reference-area R, where R is the sole child of V and where the start-edge and end-edge of the content-rectangle of R are parallel to the start-edge and end-edge of the content-rectangle of V.

Each area has the traits top-position, bottom-position, left-position, and right-position which represent the distance from the edges of its content-rectangle to the like-named edges of the nearest ancestor reference-area (or the page-viewport-area in the case of areas generated by descendants of formatting objects whose absolute-position is fixed); the left-offset and top-offset determine the amount by which a relatively-positioned area is shifted for rendering. These traits receive their values during the formatting process, or in the case of absolutely positioned areas, during refinement.

The block-progression-dimension and inline-progression-dimension of an area represent the extent of the content-rectangle of that area in each of the two relative dimensions.

Other traits include:

• the is-first and is-last traits, which are Boolean traits indicating the order in which areas are generated and returned by a given formatting object. (See [define-returned-by] . is-first is true for the first area (or only area) generated and returned by a formatting object, and is-last is true for the last area (or only area));

• the amount of space outside the border-rectangle: space-before, space-after, space-start, and space-end (though some of these may be required to be zero on certain classes of area);

  NOTE: 

  "Before", "after", "start", and "end" refer to relative directions and are defined below.

• the thickness of each of the four sides of the padding: padding-before, padding-after, padding-start, and padding-end;

• the style, thickness, and color of each of the four sides of the border: border-before, etc.;

• the background rendering of the area: background-color, background-image, and other background traits; and

• the nominal-font for an area, as determined by the font properties and the character descendants of the area's generating formatting object. (see [fontprops] )

Unless otherwise specified, the traits of a formatting object are present on each of its generated areas, and with the same value. (However, see sections [area-linebuild] and [rend-border] .)

Geometric Definitions[top]

As described above, the content-rectangle is the rectangle bounding the inside of the padding and is used to describe the constraints on the positions of descendant areas. It is possible that marks from descendant glyphs or other areas may appear outside the content-rectangle.

Related to this is the allocation-rectangle of an area, which is used to describe the constraints on the position of the area within its parent area. For an inline-area this is either the normal-allocation-rectangle or the large-allocation-rectangle. The normal-allocation-rectangle extends to the content-rectangle in the block-progression-direction and to the border-rectangle in the inline-progression-direction. The large-allocation-rectangle is the border-rectangle. Unless otherwise specified, the allocation-rectangle for an area is the normal-allocation-rectangle.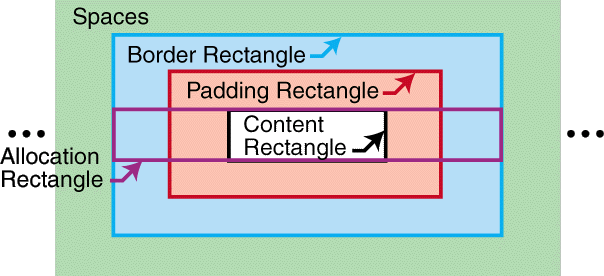

Normal-allocation-rectangle of an inline-area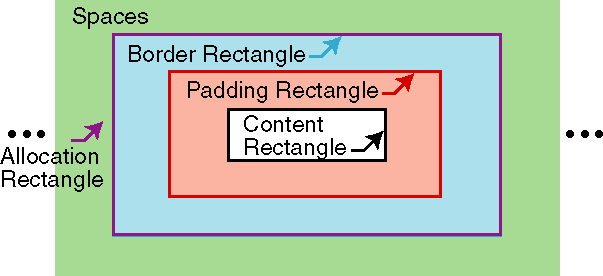

Large-allocation-rectangle of an inline-area

For a block-area, the allocation-rectangle extends to the border-rectangle in the block-progression-direction and outside the content-rectangle in the inline-progression-direction by an amount equal to the end-indent, and in the opposite direction by an amount equal to the start-indent.

NOTE: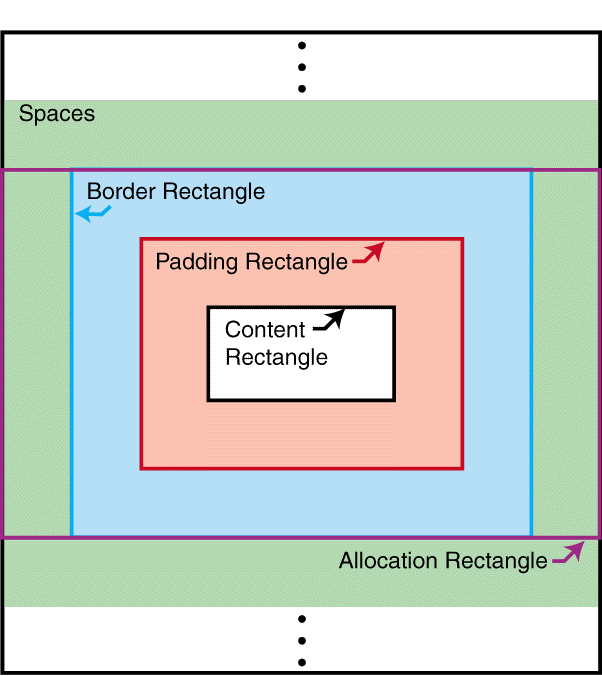 

The inclusion of space outside the border-rectangle of a block-area in the inline-progression-direction does not affect placement constraints, and is intended to promote compatibility with the CSS box model.

Allocation- and content-rectangles of a block-area

The edges of a rectangle are designated as follows:

• the before-edge is the edge occurring first in the block-progression-direction and perpendicular to it;

• the after-edge is the edge opposite the before-edge;

• the start-edge is the edge occurring first in the inline-progression-direction and perpendicular to it,

• the end-edge is the edge opposite the start-edge.

For purposes of this definition, the content-rectangle of an area uses the inline-progression-direction and block-progression-direction of that area; but the border-rectangle, padding-rectangle, and allocation-rectangle use the directions of its parent area. Thus the edges designated for the content-rectangle may not correspond to the same-named edges on the padding-, border-, and allocation-rectangles. This is important in the case of nested block-areas with different writing-modes.

The following diagram shows the correspondence between the various edge names for a mixed writing-mode example: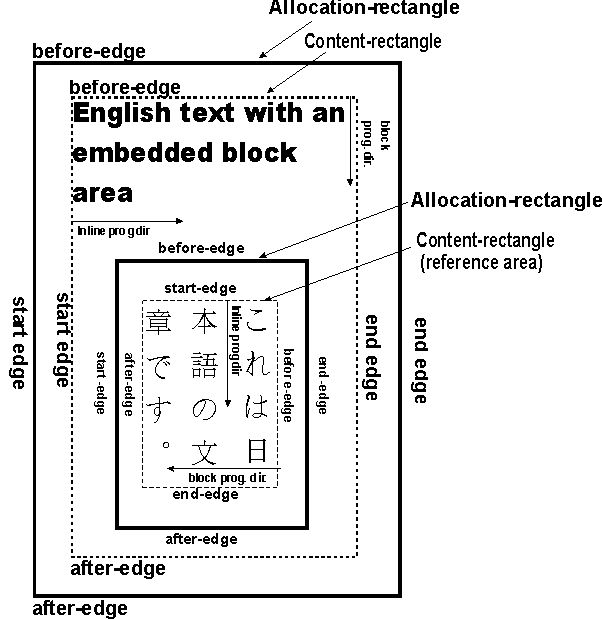

Each inline-area has an alignment-point determined by the formatter, on the start-edge of its allocation-rectangle; for a glyph-area, this is a point on the start-edge of the glyph on its alignment baseline (see below). This is script-dependent and does not necessarily correspond to the (0,0) coordinate point used for the data describing the glyph shape.

Tree Ordering[top]

In the area tree, the set of areas with a given parent is ordered. The terms initial, final, preceding, and following refer to this ordering.

In any ordered tree, this sibling order extends to an ordering of the entire tree in at least two ways.

• In the pre-order traversal order of a tree, the children of each node (their order unchanged relative to one another) follow the node, but precede any following siblings of the node or of its ancestors.

• In the post-order traversal order of a tree, the children of each node precede the node, but follow any preceding siblings of the node or of its ancestors.

"Preceding" and "following", when applied to non-siblings, will depend on the extension order used, which must be specified. However, in either of these given orders, the leaves of the tree (nodes without children) are unambiguously ordered.

Stacking Constraints[top]

This section defines the notion of block-stacking constraints and inline-stacking constraints involving areas. These are defined as ordered relations, i.e., if A and B have a stacking constraint it does not necessarily mean that B and A have a stacking constraint. These definitions are recursive in nature and some cases may depend upon simpler cases of the same definition. This is not circularity but rather a consequence of recursion. The intention of the definitions is to identify areas at any level of the tree which have only space between them.

The area-class trait is an enumerated value which is xsl-normal for an area which is stacked with other areas in sequence. A normal area is an area for which this trait is xsl-normal. A page-level-out-of-line area is an area with area-class xsl-footnote, xsl-before-float, or xsl-fixed; placement of these areas is controlled by the fo:page-sequence ancestor of its generating formatting object. A reference-level-out-of-line area is an area with area-class xsl-side-float or xsl-absolute; placement of these areas is controlled by the formatting object generating the relevant reference-area. An anchor area is an area with area-class xsl-anchor; placement of these areas is arbitrary and does not affect stacking. Areas with area-class equal to one of xsl-normal, xsl-footnote, or xsl-before-float are defined to be stackable, indicating that they are supposed to be properly stacked.

Block-stacking constraints

If P is a block-area, then there is a fence preceding P if P is a reference-area or if the border-before-width or padding-before-width of P are non-zero. Similarly, there is a fence following P if P is a reference-area or if the border-after-width or padding-after-width of P are non-zero.

If A and B are stackable areas, and S is a sequence of space-specifiers (see [spacecond] ), it is defined that A and B have block-stacking constraint S if any of the following conditions holds:

1. B is a block-area which is the first normal child of A, and S is the sequence consisting of the space-before of B.

2. A is a block-area which is the last normal child of B, and S is the sequence consisting of the space-after of A.

3. A and B are both block-areas, and either

   a. B is the next stackable sibling area of A, and S is the sequence consisting of the space-after of A and the space-before of B;

   b. B is the first normal child of a block-area P, B is not a line-area, there is no fence preceding P, A and P have a block-stacking constraint S', and S consists of S' followed by the space-before of B; or

   c. A is the last normal child of a block-area P, A is not a line-area, there is no fence following P, P and B have a block-stacking constraint S'', and S consists of the space-after of A followed by S''.

   d. A has a block-stacking constraint S' with a block-area E, E has a block-stacking constraint S'' with B, E is empty (i.e., it has zero border, padding, and block-progression-dimension, and no normal children), and S consists of S' followed by S''.

NOTE: 

The use of "stackable" in two places in the above definition allows block-stacking constraints to apply between areas of area-class xsl-before-float or xsl-footnote.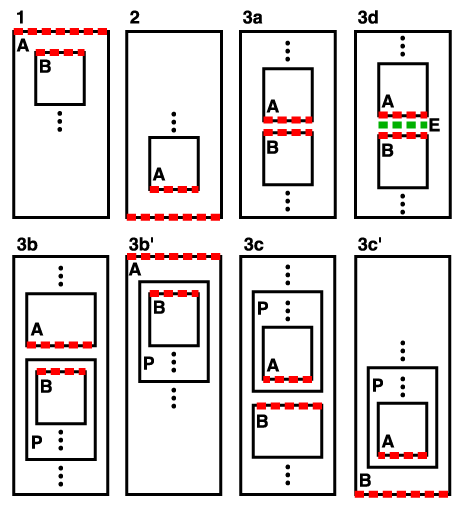

Adjacent Edges with Block-stacking

When A and B have a block-stacking constraint, the adjacent edges of A and B are an ordered pair recursively defined as:

• In case 1, the before-edge of the content-rectangle of A and the before-edge of the allocation-rectangle of B.

• In case 2, the after-edge of the allocation-rectangle of A and the after-edge of the content-rectangle of B.

• In case 3a, the after-edge of the allocation-rectangle of A and the before-edge of the allocation-rectangle of B.

• In case 3b, the first of the adjacent edges of A and P, and the before-edge of the allocation-rectangle of B.

• In case 3c, the after-edge of the allocation-rectangle of A and the second of the adjacent edges of P and B.

• In case 3d, the first of the adjacent edges of A and E, and the second of the adjacent edges of E and B.

Example. In this diagram each node represents a block-area. Assume that all padding and border widths are zero, and none of the areas are reference-areas. Then P and A have a block-stacking constraint, as do A and B, A and C, B and C, C and D, D and B, B and E, D and E, and E and P; these are the only pairs in the diagram having block-stacking constraints. If B had non-zero padding-after, then D and E would not have any block-stacking constraint (though B and E would continue to have a block-stacking constraint).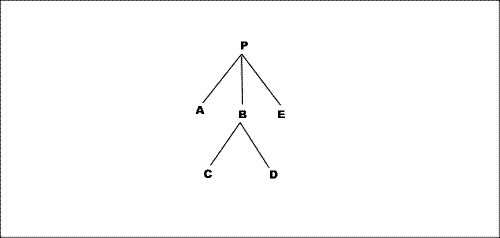

Block-stacking constraint example

Inline-stacking constraints.

This section will recursively define the inline-stacking constraints between two areas (either two inline-areas or one inline-area and one line-area), together with the notion of fence preceding and fence following; these definitions are interwoven with one another. This parallels the definition for block-stacking constraints, but with the additional complication that we may have a stacking constraint between inline-areas which are stacked in opposite inline-progression-directions. (This is not an issue for block-stacking constraints because a block-area which is not a reference-area may not have a block-progression-direction different from that of its parent.)

If P and Q have an inline-stacking constraint, then P has a fence preceding Q if P is a reference-area or has non-zero border-width or padding-width at the first adjacent edge of P and Q. Similarly, Q has a fence following P if Q is a reference-area or has non-zero border-width or padding-width at the second adjacent edge of P and Q.

If A and B are normal areas, and S is a sequence of space-specifiers, it is defined that A and B have inline-stacking constraint S if any of the following conditions holds:

1. A is an inline-area or line-area, B is an inline-area which is the first normal child of A, and S is the sequence consisting of the space-start of B.

2. B is an inline-area or line-area, A is an inline-area which is the last normal child of B, and S is the sequence consisting of the space-end of A.

3. A and B are each either an inline-area or a line-area, and either

   a. both A and B are inline-areas, B is the next normal sibling area of A, and S is the sequence consisting of the space-end of A and the space-start of B;

   b. B is an inline-area which is the first normal child of an inline-area P, P has no fence following A, A and P have an inline-stacking constraint S', the inline-progression-direction of P is the same as the inline-progression-direction of the nearest common ancestor area of A and P, and S consists of S' followed by the space-start of B.

   c. A is an inline-area which is the last normal child of an inline-area P, P has no fence preceding B, P and B have an inline-stacking constraint S'', the inline-progression-direction of P is the same as the inline-progression-direction of the nearest common ancestor area of P and B, and S consists of the space-end of A followed by S''.

   d. B is an inline-area which is the last normal child of an inline-area P, P has no fence following A, A and P have an inline-stacking constraint S', the inline-progression-direction of P is opposite to the inline-progression-direction of the nearest common ancestor area of A and P, and S consists of S' followed by the space-end of B.

   e. A is an inline-area which is the first normal child of an inline-area P, P has no fence preceding B, P and B have an inline-stacking constraint S'', the inline-progression-direction of P is opposite to the inline-progression-direction of the nearest common ancestor area of P and B, and S consists of the space-start of A followed by S''.

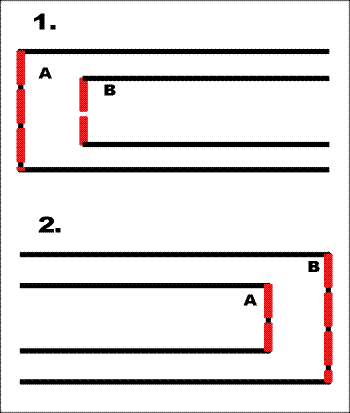
Adjacent Edges with Inline-stacking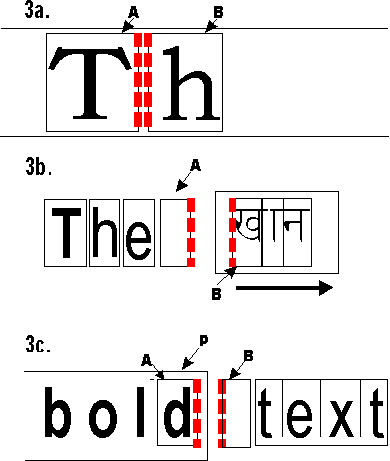

Adjacent Edges with Inline-stacking, continued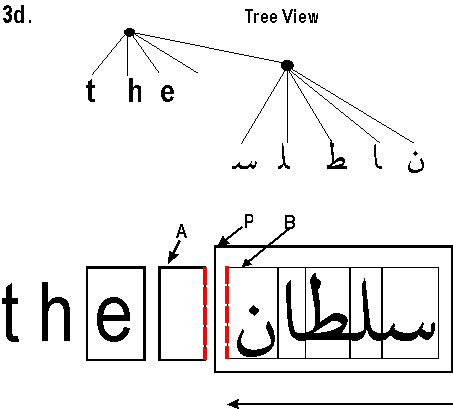

Mixed English and Arabic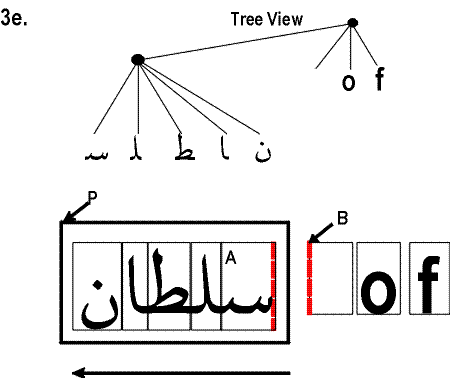

Mixed English and Arabic

When A and B have an inline-stacking constraint, the adjacent edges of A and B are an ordered pair defined as:

• In case 1, the start-edge of the content-rectangle of A and the start-edge of the allocation-rectangle of B.

• In case 2, the end-edge of the allocation-rectangle of A and the end-edge of the content-rectangle of B.

• In case 3a, the end-edge of the allocation-rectangle of A and the start-edge of the allocation-rectangle of B.

• In case 3b, the first of the adjacent edges of A and P, and the start-edge of the allocation-rectangle of B.

• In case 3c, the end-edge of the allocation-rectangle of A and the second of the adjacent edges of P and B.

• In case 3d, the first of the adjacent edges of A and P, and the end-edge of the allocation-rectangle of B.

• In case 3e, the start-edge of the allocation-rectangle of A and the second of the adjacent edges of P and B.

Two areas are adjacent if they have a block-stacking constraint or an inline-stacking constraint. It follows from the definitions that areas of the same type (inline or block) can be adjacent only if all their non-common ancestors are also of the same type (up to but not including their nearest common ancestor). Thus, for example, two inline-areas which reside in different line-areas are never adjacent.

An area A begins an area P if A is a descendant of P and P and A have either a block-stacking constraint or an inline-stacking constraint. In this case the second of the adjacent edges of P and A is defined to be a leading edge in P. A space-specifier which applies to the leading edge is also defined to begin P.

Similarly, An area A ends an area P if A is a descendant of P and A and P have either a block-stacking constraint or an inline-stacking constraint. In this case the first of the adjacent edges of A and P is defined to be a trailing edge in P. A space-specifier which applies to the trailing edge is also defined to end P.

Font Baseline Tables[top]

Each script has its preferred "baseline" for aligning glyphs from that script. Western scripts typically use an "alphabetic" baseline that touches at or near the bottom of capital letters. Further, for each font there is a preferred way of aligning embedded glyphs from different scripts, e.g., for a Western font there are separate baselines for aligning embedded ideographic or Indic glyphs.

Each block-area and inline-area has a dominant-baseline-identifier trait whose value is a baseline identifier corresponding to the type of alignment expected for inline-area descendants of that area, and each inline-area has an alignment-baseline which specifies how the area is aligned to its parent. These traits are interpreted as described in section [font-model] .

For each font, an actual-baseline-table maps these identifiers to points on the start-edge of the area. By abuse of terminology, the line in the inline-progression-direction through the point corresponding to the dominant-baseline-identifier is called the "dominant baseline."